Multiple sequence alignment

Multiple sequence alignment#

Sequences come in families#

Sequences come in families that share common evolutionary origin. For example, in the previous hands-on, we looked at a family of ACE2 sequences.

Here is an example of a family of human cyclophilin proteins:

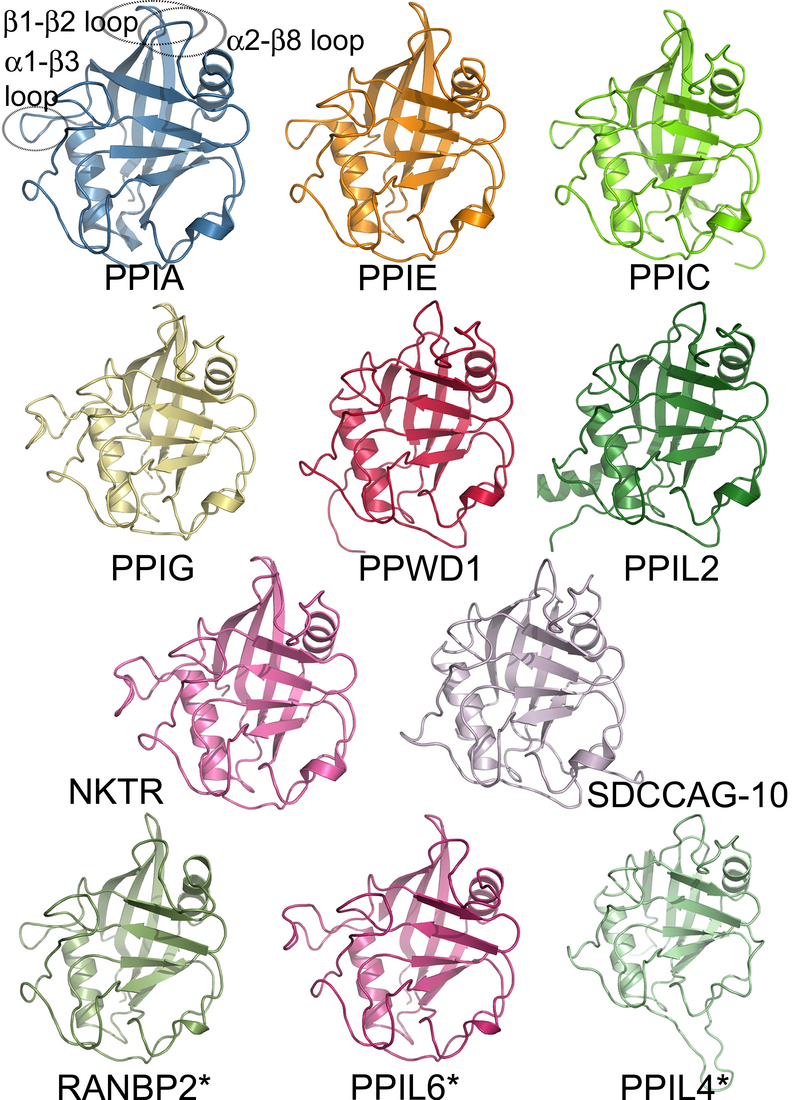
../../_images/human_cyclophilin_family.png — Fig. 34 A family of human cyclophilin proteins.
Source: (https://en.wikipedia.org/wiki/Protein_family#/media/File:Structural_coverage_of_the_human_cyclophilin_family.png).#

Here is a family of OmpA domain found in proteins that are localized in the outer membrane of many Gram-negative bacteria.

../../_images/ompa_domain.png — Fig. 35 OmpA domain family. Source: PFAM PF00691 https://www.ebi.ac.uk/interpro/entry/pfam/PF00691/\#

Here is the Tn3 family of mobile genetic elements found in many bacteria and known to carry anti-biotic resistance genes.

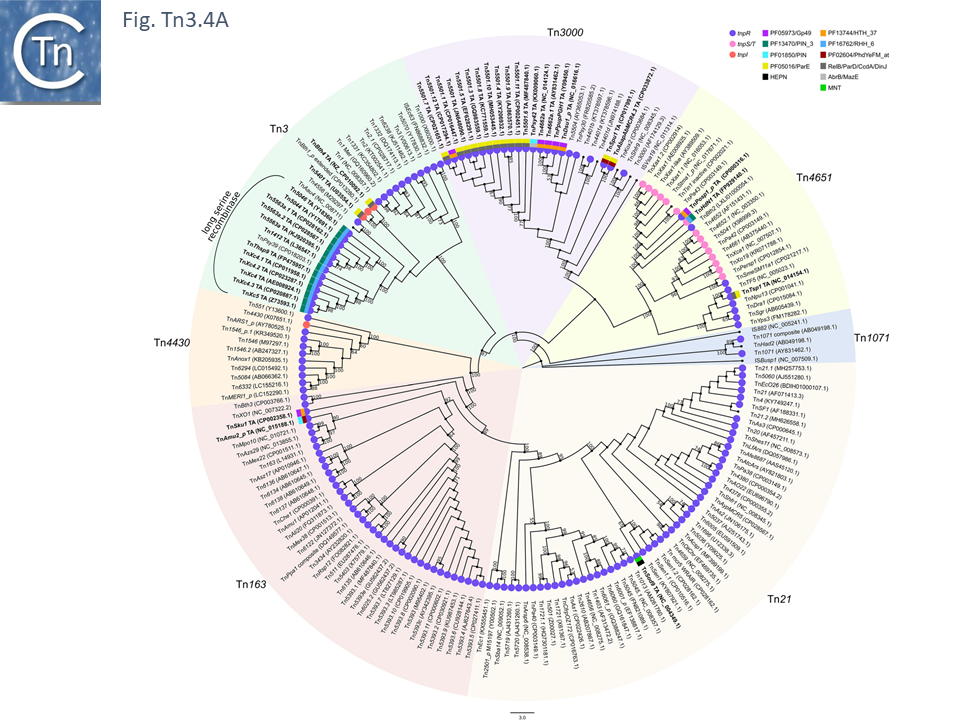
../../_images/tn3_family.png — Fig. 36 Tn3 family of mobile genetic elements found in many bacteria.
Source: https://tncentral.ncc.unesp.br/TnPedia/index.php/Transposons_families/Tn3_family.
TnPedia Team. (2025). TnPedia – Chapter: The Tn3 Family of Prokaryotic Transposons. Zenodo. https://doi.org/10.5281/zenodo.15566224\#

Aligning multiple sequences#

Multiple sequence alignment (MSA) extends the idea of pairwise sequence alignment to more than 2 sequences. That is, given a family of sequences, we wish to arrange sequences into columns of homologous residues, much like in the pairwise alignment case.

The figure below shows a portion of an MSA of ACE2 orthologs. You can see that one MSA of \(n\) sequences provides a lot of information that would be hard to extract from pairwise alignments of all the \(n(n-1)/2\) pairs.

../../_images/ace2_msa_1-51.svg — Fig. 37 The first 51 columns of a multiple sequence alignment of ACE2 orthologs, computed by MUSCLE, visualized by Jalview using the Clustal color scheme.#

What is an MSA used for?#

An MSA is fundamental to studying the evolution of the family. Specifically, they can be used:

For computing nucleotide and amino acid substitution rates.
For building a profile hidden Markov model which is a statistical model of a family of sequences.
For building a phylogenetic tree, etc.

Computing an MSA#

MSA computation, like the pairwise alignment problem, can be modeled as a discrete optimization problem. This requires first defining a scoring scheme. One way to score an MSA is to simply take the sum of the scores of \(n(n-1)/2\) pairwise alignments that can be obtained from the MSA. Unfortunately, under this scoring scheme, finding an optimal MSA is NP-hard. This opens the problem to popular search meta-heuristics like simulated annealing and genetic algorithm. However, this approach is slow. Most modern MSA tools rely on a different kind of heuristics called progressive alignment.

Progressive alignment#

Overview#

As the name suggests, this technique grows an MSA by progressively adding more sequences to it. It can be summarized as:

Progressive alignment

Step 1: Compute pairwise distances between each pair of sequences.
Step 2: Build a bifurcating guide tree which has the input sequences as its leaves.
Step 3: For each internal node, merge the alignments at its two children.
Step 4: Return the alignment at the root

Here’s an illustration of the process:

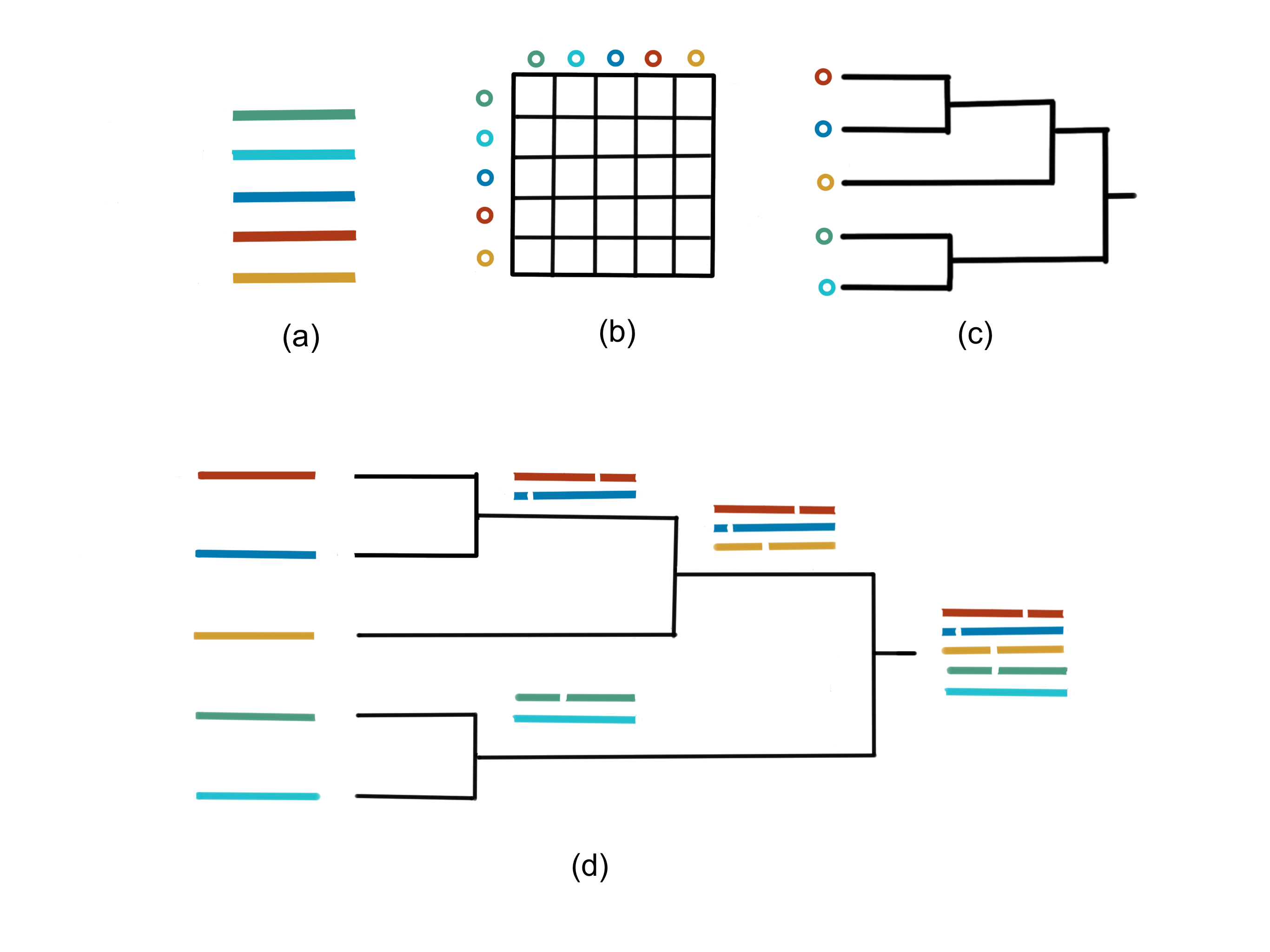
../../_images/progressive_msa.png — Fig. 38 Overview of progressive multiple sequence alignment method. Pairwise distances (b) of input sequences (a) are used to compute a guide tree (c) which dictates the progression of the MSA computation. At an internal node of the guide tree, alignments (or sequences) at its children node are merged into a new alignment of the all the sequences in the subtree rooted at that internal node.#

Let’s add a few more details to these.

Guide tree#

The guide tree can computed using something simple like UPGMA. Computing a tree requires pairwise distances that can be computed using pairwise alignments, but that would be slow. Faster methods involve computing distances based on common k-mers.

There is also an interesting claim that simple chained guide tree work just as well, and we don’t need to worry too much about finding a “good” guide tree.

Merging two alignments#

At an internal node, depending on what the children nodes are, we need to align two alignments, or align a sequence to an alignment, or align two sequences.

This can be done by representing an alignment as a profile, which is a matrix of residue frequencies in each column of the alignment. Take for example the columsn 20-24 of the MSA of the ACE2 sequences shown above.

\( \begin{array}{ccccc} 20 & 21 & 22 & 23 & 24 \\ \texttt{T} & \texttt{I} & \texttt{E} & \texttt{E} & \texttt{Q} \\ \texttt{V} & \texttt{T} & \texttt{Q} & \texttt{E} & \texttt{-} \\ \texttt{T} & \texttt{T} & \texttt{E} & \texttt{D} & \texttt{E} \\ \texttt{T} & \texttt{T} & \texttt{E} & \texttt{E} & \texttt{L} \\ \texttt{T} & \texttt{T} & \texttt{E} & \texttt{E} & \texttt{L} \\ \texttt{T} & \texttt{T} & \texttt{E} & \texttt{E} & \texttt{L} \\ \end{array} \)

Their profile representation looks like:

\( \begin{array}{ccccc} 20 & 21 & 22 & 23 & 24 \\ \texttt{T}: 5/6 & \texttt{I}: 1/6 & \texttt{E}: 5/6& \texttt{E}: 5/6& \texttt{Q}: 1/6 \\ \texttt{V}: 1/6 & \texttt{T}: 5/6 & \texttt{Q}: 1/6& \texttt{D}: 1/6 & \texttt{L}: 3/6\\ & & & & \texttt{E}: 1/6\\ & & & & \texttt{-}: 1/6 \end{array} \)

Aligning two profiles can then be done using the same dynamic programming algorithm as for aligning two sequences, but with the scores weighted by the frequency of the residue/gap in the column.