Global alignment

Global alignment#

Use cases#

Aligning two homologous genes to identify evolutionary events.
Computing evolutionary distance between two homologous genes, which can be used for multiple sequence alignment and phylogenetic tree construction (more on this in later sections).

Computational problem formulation#

We can formulate the problem of finding a global alignment between two sequences as a discrete optimization problem, in which we define a way to score an alignment and the goal would be to find a highest scoring one.

Scoring an alignment#

Shown below are two different alignments of the same pair of sequences. Which one is a better alignment, i.e. which one seems to be a better hypothesis of how these sequences have evolved?

../../_images/two_alignments.svg — Fig. 24 Two alignments of the same sequence pair. Which one should score higher?#

The commonly used scoring scheme has two components: (1) a substitution matrix \(M = [m_{xy}]\), where \(m_{xy}\) is the score for an alignment column containing residues \(x\) and \(y\) in the first and second sequence, respectively, and (2) a gap penalty to score the insertions and deletions (also called indels).

Shown below is a substitution matrix called BLOSUM-62 often used for protein sequence alignment. More later on where these come from.

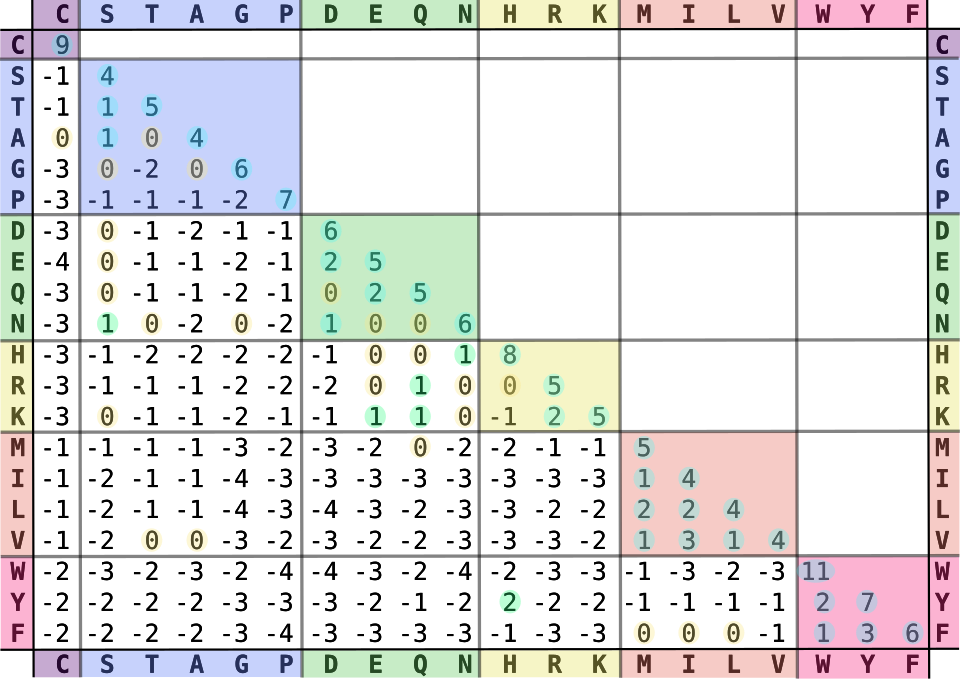
../../_images/960px-Blosum62-dayhoff-ordering.svg.png — Fig. 25 BLOSUM-62 substitution matrix.
Source: https://en.wikipedia.org/wiki/BLOSUM#/media/File:Blosum62-dayhoff-ordering.svg#

A simple choice of gap penalty is a linear one in which a length-\(l\) gap is given a penatly of \(gl\) for some positive number \(g\). It is however typical to use something called an affine gap penalty in which a length-\(l\) gap gets a penalty of \(o + e (l-1)\), where \(o,e\) are gap open and gap extension penalties. This is based partly on the observation of indel size distributions and partly because it is easier to fit it into the dynamic programming scheme discussed below.

Brute-force? No thanks.#

The number of possible global alignments between two sequences is very large. More specifically, for two sequences both of length \(n\), the number of global alignments between them is \(\Omega(3^n)\) and \(O(1+\sqrt{2})^{2n}\) (https://doi.org/10.1080/10425170310001617894). So brute-force search is clearly not feasible.

Luckily, finding a max-scoring global alignment under the scoring scheme described above yields nicely to dynamic programming.

Needleman-Wunsch algorithm for global alignment#

Optimal substructure property#

Let \(A\) and \(B\) be the two input sequences of lengths \(m\) and \(n\), respectively. For a sequence \(A\), let \(A[i]\) denote its \(i\)-th residue and \(A[i:j]\) denote the substring \(A[i], A[i+1],\ldots, A[j]\). For simplicity, let’s assume linear gap penalty for now.

Consider an optimal global alignment between the prefixes \(A[1:i]\) and \(B[1:j]\) and let \(S_{ij}\) be its score. The rightmost column of such an alignment can be one of three cases: it aligns \(A[i]\) with \(B[j]\), \(A[i]\) is aligned to a gap character, or \(B[j]\) is aligned to a gap character. The sub-alignment left of the rightmost column must be an optimal alignment (see Figure below).

../../_images/optimal_substructure_property.svg — Fig. 26 Optimal substructure property#

Thus we can obtain the following recurrence:

\[\begin{split} \begin{align} S_{ij} &= \max \begin{cases} S_{i-1,j-1} + m_{A[i],B[j]}\\ S_{i-1,j} + g\\ S_{i,j-1} + g \end{cases} \\[2em] \end{align}\end{split}\]

The base cases are:

\[\begin{split} \begin{align} S_{0,j} &= gj \text{ for } 0 \leq j \leq n \\ S_{i,0} &= gi \text{ for } 0 \leq i \leq m \end{align}\end{split}\]

Bottom-up computation#

The computation of \(S_{ij}\) can be visualized as a matrix with each cell corresponding to \(S_{ij}\). Computing a cell depends only on 3 other cells: one immediately above, one to the left, and one diagonally to the left. There this matrix can be computed by filling in the rows from top to bottom and each row filling in the cells from left to right. Are there other orders in which to compute the cells?

Obtaining an optimal alignment#

The computation of \(S_{ij}\) just gives the optimal global alignment score. To obtain the actual optimal alignment, we need remember which of the 3 cases gives the maximum, and use that information to perform traceback.

Demo#

Here is an online demonstration.

Time complexity#

Let \(m,n\) be the lengths of sequences \(A\),\(B\), respectively. Since there are \(\Theta(mn)\) cells to compute and each cell takes \(\Theta(1)\) to compute each cell, the running time is \(\Theta(mn)\).